Home  ›  Match the Following Properties of Liquids to What They Indicate About the Relative Strength

Match the Following Properties of Liquids to What They Indicate About the Relative Strength

Written By Saturday, April 2, 2022 Add Comment Edit

Liquids and Solids

58 Properties of Liquids

Learning Objectives

By the end of this section, you lot will be able to:

  • Distinguish between adhesive and cohesive forces
  • Define viscosity, surface tension, and capillary ascent
  • Draw the roles of intermolecular bonny forces in each of these properties/phenomena

When y'all pour a glass of water, or fill up a car with gasoline, yous discover that water and gasoline flow freely. But when you pour syrup on pancakes or add oil to a car engine, you note that syrup and motor oil do non flow as readily. The viscosity of a liquid is a measure of its resistance to flow. Water, gasoline, and other liquids that flow freely have a low viscosity. Dear, syrup, motor oil, and other liquids that do non flow freely, like those shown in (Figure), accept college viscosities. We can measure viscosity by measuring the charge per unit at which a metal ball falls through a liquid (the ball falls more than slowly through a more glutinous liquid) or past measuring the rate at which a liquid flows through a narrow tube (more viscous liquids flow more slowly).

(a) Honey and (b) motor oil are examples of liquids with high viscosities; they menstruation slowly. (credit a: modification of work by Scott Bauer; credit b: modification of work by David Nagy)

Two photographs are shown and labeled

The IMFs between the molecules of a liquid, the size and shape of the molecules, and the temperature determine how easily a liquid flows. As (Figure) shows, the more structurally complex are the molecules in a liquid and the stronger the IMFs between them, the more difficult it is for them to move past each other and the greater is the viscosity of the liquid. As the temperature increases, the molecules move more rapidly and their kinetic energies are better able to overcome the forces that hold them together; thus, the viscosity of the liquid decreases.

Viscosities of Common Substances at 25 °C
Substance Formula Viscosity (mPa·south)
water H2O 0.890
mercury Hg i.526
ethanol C2H5OH i.074
octane C8H18 0.508
ethylene glycol CH2(OH)CH2(OH) sixteen.1
beloved variable ~2,000–10,000
motor oil variable ~fifty–500

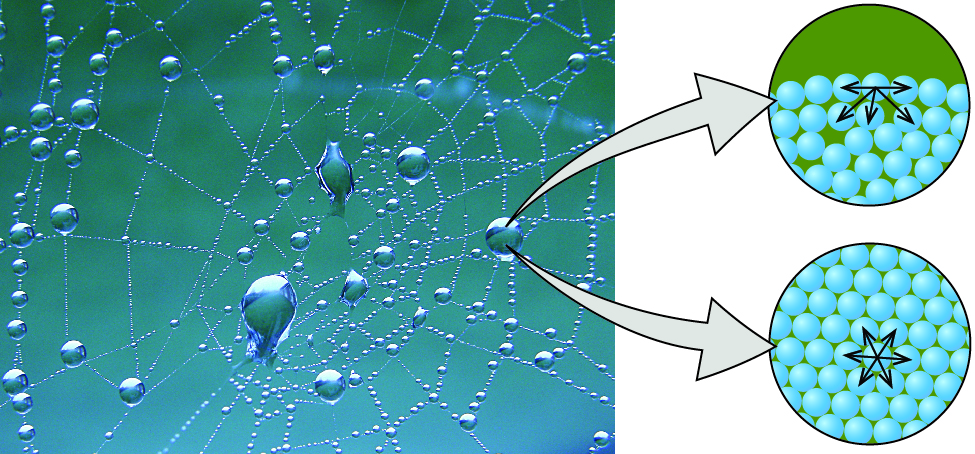
The various IMFs between identical molecules of a substance are examples of cohesive forces. The molecules within a liquid are surrounded by other molecules and are attracted equally in all directions by the cohesive forces inside the liquid. Nonetheless, the molecules on the surface of a liquid are attracted only by virtually one-one-half equally many molecules. Because of the unbalanced molecular attractions on the surface molecules, liquids contract to form a shape that minimizes the number of molecules on the surface—that is, the shape with the minimum surface area. A small drop of liquid tends to assume a spherical shape, equally shown in (Effigy), because in a sphere, the ratio of surface area to volume is at a minimum. Larger drops are more greatly affected past gravity, air resistance, surface interactions, and and then on, and as a upshot, are less spherical.

Attractive forces result in a spherical h2o drop that minimizes surface area; cohesive forces hold the sphere together; adhesive forces keep the driblet attached to the spider web. (credit photo: modification of work by "OliBac"/Flickr)

A photo of a spider's web with droplets of water attached to it is shown. Two images are shown the right of the photo and arrows lead from the photo to the images. The upper image shows twenty eight blue spheres stacked one atop the other in the bottom of a circular background. Five arrows are drawn pointing to the sides and downward from the sphere in the top middle of the drawing. The lower image shows another circular background of the same size as the first, but this time the blue spheres fill the image and are packed closely together. A sphere in the middle has six arrows pointing in all directions away from it.

Surface tension is defined as the energy required to increase the surface area of a liquid, or the strength required to increase the length of a liquid surface by a given amount. This property results from the cohesive forces between molecules at the surface of a liquid, and it causes the surface of a liquid to behave like a stretched rubber membrane. Surface tensions of several liquids are presented in (Figure). Among common liquids, water exhibits a distinctly high surface tension due to stiff hydrogen bonding between its molecules. As a result of this loftier surface tension, the surface of water represents a relatively "tough pare" that can withstand considerable strength without breaking. A steel needle carefully placed on h2o will float. Some insects, like the ane shown in (Figure), even though they are denser than water, move on its surface considering they are supported by the surface tension.

Surface Tensions of Common Substances at 25 °C
Substance Formula Surface Tension (mN/1000)
h2o H2O 71.99
mercury Hg 458.48
ethanol CtwoH5OH 21.97
octane C8H18 21.xiv
ethylene glycol CH2(OH)CHii(OH) 47.99

Surface tension (right) prevents this insect, a "water strider," from sinking into the water.

A photo and a diagram as shown and a right-facing arrow leads from the photo to the image. The photo shows an insect standing on the surface of a sample of water. The image shows a square background that is two thirds covered in blue spheres that are closely packet together. A brown line starts at the upper left corner of the background and rests on top of the first row of spheres. The sphere directly under this low point of the line has four arrows drawn on it that face to both sides and downward. A sphere in the bottom center of the image has six arrows drawn on it that all face outward in different directions.

The IMFs of attraction between two different molecules are called adhesive forces. Consider what happens when water comes into contact with some surface. If the agglutinative forces between water molecules and the molecules of the surface are weak compared to the cohesive forces between the h2o molecules, the water does not "wet" the surface. For example, water does not wet waxed surfaces or many plastics such as polyethylene. H2o forms drops on these surfaces considering the cohesive forces within the drops are greater than the adhesive forces between the water and the plastic. Water spreads out on glass because the agglutinative forcefulness betwixt water and drinking glass is greater than the cohesive forces within the water. When water is confined in a glass tube, its meniscus (surface) has a concave shape because the water wets the drinking glass and creeps upward the side of the tube. On the other mitt, the cohesive forces between mercury atoms are much greater than the adhesive forces between mercury and drinking glass. Mercury therefore does not wet glass, and it forms a convex meniscus when confined in a tube considering the cohesive forces within the mercury tend to draw information technology into a drop ((Effigy)).

Differences in the relative strengths of cohesive and adhesive forces event in different meniscus shapes for mercury (left) and water (correct) in glass tubes. (credit: Mark Ott)

This figure shows two test tubes. The test tube on the left contains mercury with a meniscus that rounds up. The test tube on the right contains water with a meniscus that rounds down.

If you identify ane terminate of a newspaper towel in spilled wine, every bit shown in (Figure), the liquid wicks up the newspaper towel. A similar procedure occurs in a cloth towel when y'all use it to dry out off afterwards a shower. These are examples of capillary activity—when a liquid flows within a porous material due to the allure of the liquid molecules to the surface of the material and to other liquid molecules. The agglutinative forces between the liquid and the porous material, combined with the cohesive forces within the liquid, may be strong plenty to motion the liquid upward confronting gravity.

Wine wicks upwards a paper towel (left) because of the strong attractions of water (and ethanol) molecules to the −OH groups on the towel's cellulose fibers and the potent attractions of water molecules to other water (and ethanol) molecules (right). (credit photo: modification of work by Marking Blaser)

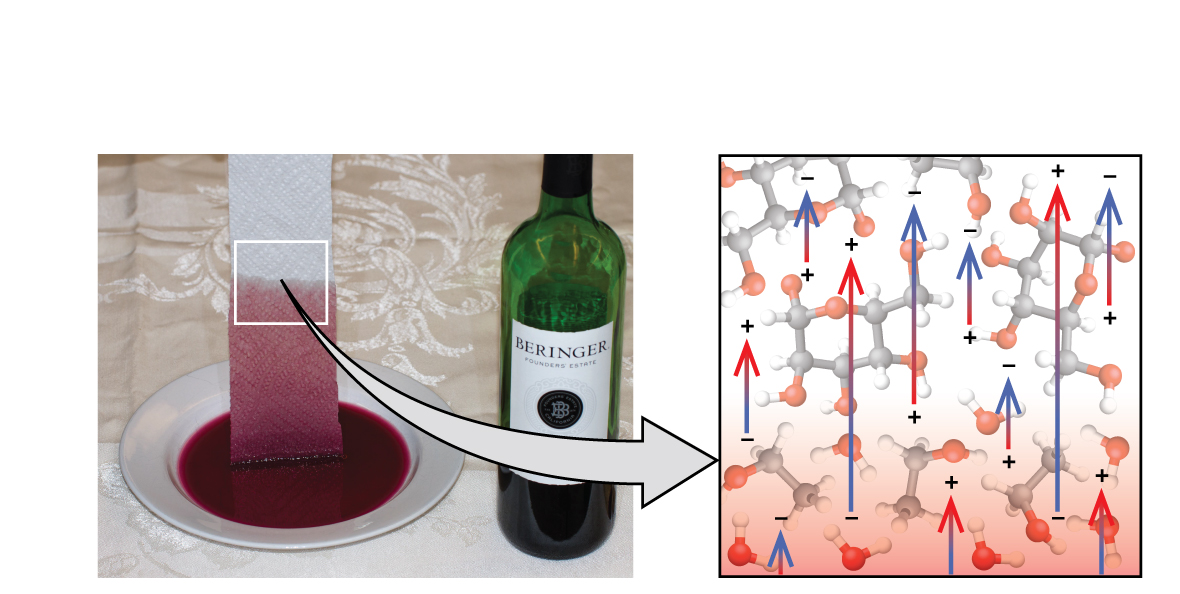
A photo and a diagram are shown. In the photo, a paper towel is dipped into a bowl full of a red liquid sitting on a countertop. The red liquid is traveling up the lower part of the paper towel, and this section of the photo has a square drawn around it. A right-facing arrow leads from this square to the image. The image is square and has a background of two types of molecules, mixed together. The first type of molecule is composed of two bonded black spheres, one of which is single bonded to three white spheres and one of which is single bonded to two white spheres and a red sphere that is itself bonded to a white sphere. The other type of molecule is composed of six black spheres bonded together in a row and bonded to other red and white spheres. Six upward-facing arrows are drawn on top of this background. They have positive signs on their lower ends and negative signs on their heads. Four upward-facing arrows are drawn with their signs reversed.

Towels soak up liquids like water because the fibers of a towel are fabricated of molecules that are attracted to water molecules. About cloth towels are made of cotton wool, and paper towels are generally made from newspaper pulp. Both consist of long molecules of cellulose that contain many −OH groups. H2o molecules are attracted to these −OH groups and form hydrogen bonds with them, which draws the H2O molecules upward the cellulose molecules. The h2o molecules are also attracted to each other, so large amounts of water are fatigued up the cellulose fibers.

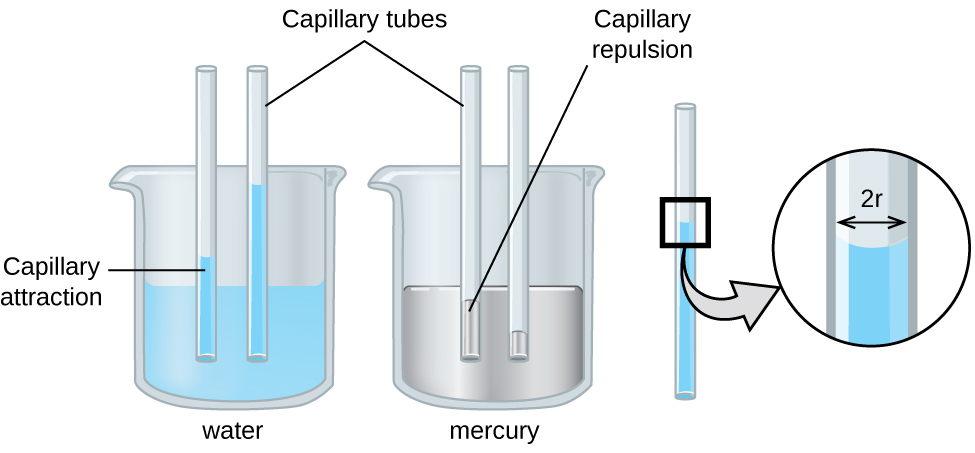
Capillary activeness can also occur when one end of a modest diameter tube is immersed in a liquid, as illustrated in (Figure). If the liquid molecules are strongly attracted to the tube molecules, the liquid creeps upward the inside of the tube until the weight of the liquid and the adhesive forces are in rest. The smaller the diameter of the tube is, the college the liquid climbs. Information technology is partly by capillary action occurring in plant cells chosen xylem that water and dissolved nutrients are brought from the soil upwards through the roots and into a plant. Capillary activeness is the footing for sparse layer chromatography, a laboratory technique commonly used to separate small quantities of mixtures. Yous depend on a constant supply of tears to keep your optics lubricated and on capillary activeness to pump tear fluid away.

Depending upon the relative strengths of agglutinative and cohesive forces, a liquid may rising (such as water) or fall (such as mercury) in a glass capillary tube. The extent of the rise (or autumn) is straight proportional to the surface tension of the liquid and inversely proportional to the density of the liquid and the radius of the tube.

An image of two beakers and a tube is shown. The first beaker, drawn on the left and labeled

The summit to which a liquid will rise in a capillary tube is determined by several factors as shown in the post-obit equation:

h=\phantom{\rule{0.2em}{0ex}}\frac{2T\phantom{\rule{0.2em}{0ex}}\text{cos}\phantom{\rule{0.2em}{0ex}}\theta }{r\rho g}

In this equation, h is the height of the liquid inside the capillary tube relative to the surface of the liquid exterior the tube, T is the surface tension of the liquid, θ is the contact angle between the liquid and the tube, r is the radius of the tube, ρ is the density of the liquid, and g is the acceleration due to gravity, 9.8 grand/s2. When the tube is made of a textile to which the liquid molecules are strongly attracted, they volition spread out completely on the surface, which corresponds to a contact angle of 0°. This is the situation for water ascent in a glass tube.

Capillary Ascension At 25 °C, how loftier will water rise in a glass capillary tube with an inner diameter of 0.25 mm?

For h2o, T = 71.99 mN/m and ρ = 1.0 grand/cm3.

Solution The liquid will rise to a height h given by: h=\phantom{\rule{0.2em}{0ex}}\frac{2T\phantom{\rule{0.2em}{0ex}}\text{cos}\phantom{\rule{0.2em}{0ex}}\theta }{r\rho g}

The Newton is defined as a kg m/s2, and and then the provided surface tension is equivalent to 0.07199 kg/s2. The provided density must exist converted into units that will abolish appropriately: ρ = yard kg/yard3. The diameter of the tube in meters is 0.00025 yard, so the radius is 0.000125 m. For a glass tube immersed in water, the contact angle is θ = 0°, so cos θ = 1. Finally, dispatch due to gravity on the earth is g = nine.viii m/s2. Substituting these values into the equation, and cancelling units, nosotros have:

h=\phantom{\rule{0.2em}{0ex}}\frac{2\left(0.07199\phantom{\rule{0.2em}{0ex}}{\text{kg/s}}^{2}\right)}{\left(0.000125\phantom{\rule{0.2em}{0ex}}\text{m}\right)\left(1000\phantom{\rule{0.2em}{0ex}}{\text{kg/m}}^{3}\right)\left(9.8\phantom{\rule{0.2em}{0ex}}{\text{m/s}}^{2}\right)}\phantom{\rule{0.2em}{0ex}}=0.12\phantom{\rule{0.2em}{0ex}}\text{m}=\phantom{\rule{0.2em}{0ex}}\text{12 cm}

Check Your Learning Water rises in a glass capillary tube to a height of 8.iv cm. What is the diameter of the capillary tube?

Respond:

bore = 0.36 mm

Biomedical Applications of Capillary Activity

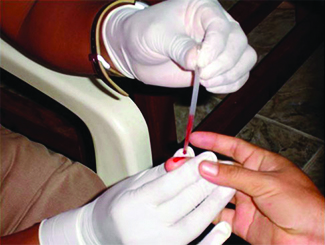
Many medical tests require cartoon a pocket-size amount of blood, for example to determine the amount of glucose in someone with diabetes or the hematocrit level in an athlete. This procedure tin be easily done because of capillary action, the ability of a liquid to menstruation up a small tube against gravity, every bit shown in (Figure). When your finger is pricked, a drop of claret forms and holds together due to surface tension—the unbalanced intermolecular attractions at the surface of the driblet. And so, when the open stop of a narrow-bore glass tube touches the drop of blood, the agglutinative forces between the molecules in the blood and those at the drinking glass surface draw the blood up the tube. How far the blood goes upwardly the tube depends on the diameter of the tube (and the type of fluid). A small tube has a relatively large surface area for a given volume of blood, which results in larger (relative) bonny forces, assuasive the blood to be drawn farther up the tube. The liquid itself is held together past its own cohesive forces. When the weight of the liquid in the tube generates a downward force equal to the upward force associated with capillary activeness, the liquid stops rising.

Blood is nerveless for medical analysis past capillary activeness, which draws blood into a small diameter glass tube. (credit: modification of work past Centers for Disease Control and Prevention)

A photograph shows a person's hand being held by a person wearing medical gloves. A thin glass tube is pressed against the persons finger and blood is moving up the tube.

Central Concepts and Summary

The intermolecular forces between molecules in the liquid state vary depending upon their chemical identities and event in corresponding variations in various physical properties. Cohesive forces between like molecules are responsible for a liquid's viscosity (resistance to flow) and surface tension (elasticity of a liquid surface). Agglutinative forces between the molecules of a liquid and unlike molecules composing a surface in contact with the liquid are responsible for phenomena such equally surface wetting and capillary rise.

Key Equations

  • h=\phantom{\rule{0.2em}{0ex}}\frac{2T\phantom{\rule{0.2em}{0ex}}\text{cos}\phantom{\rule{0.2em}{0ex}}\theta }{r\rho g}

Chemistry End of Chapter Exercises

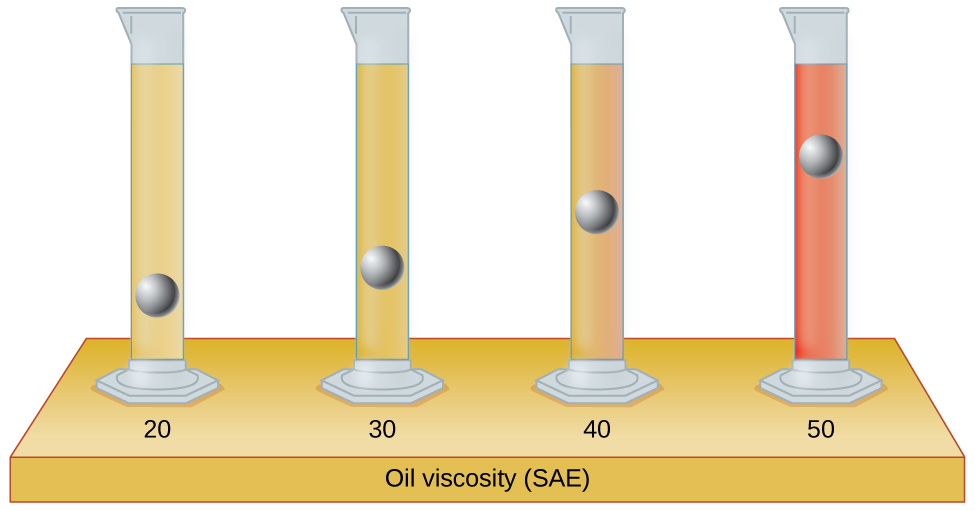
The test tubes shown here contain equal amounts of the specified motor oils. Identical metal spheres were dropped at the aforementioned time into each of the tubes, and a brief moment later, the spheres had fallen to the heights indicated in the illustration.

Rank the motor oils in society of increasing viscosity, and explain your reasoning:

An image of four graduated cylinders sitting on a table labeled

Although steel is denser than water, a steel needle or paper clip placed advisedly lengthwise on the surface of still water tin can be fabricated to float. Explain at a molecular level how this is possible.

(credit: Cory Zanker)

A photo shows a close-up, above-view, of a needle lying on the surface of a sample of water.

The water molecules have strong intermolecular forces of hydrogen bonding. The water molecules are thus attracted strongly to one some other and exhibit a relatively large surface tension, forming a blazon of "skin" at its surface. This pare tin can support a bug or paper clip if gently placed on the h2o.

The surface tension and viscosity values for diethyl ether, acetone, ethanol, and ethylene glycol are shown here.

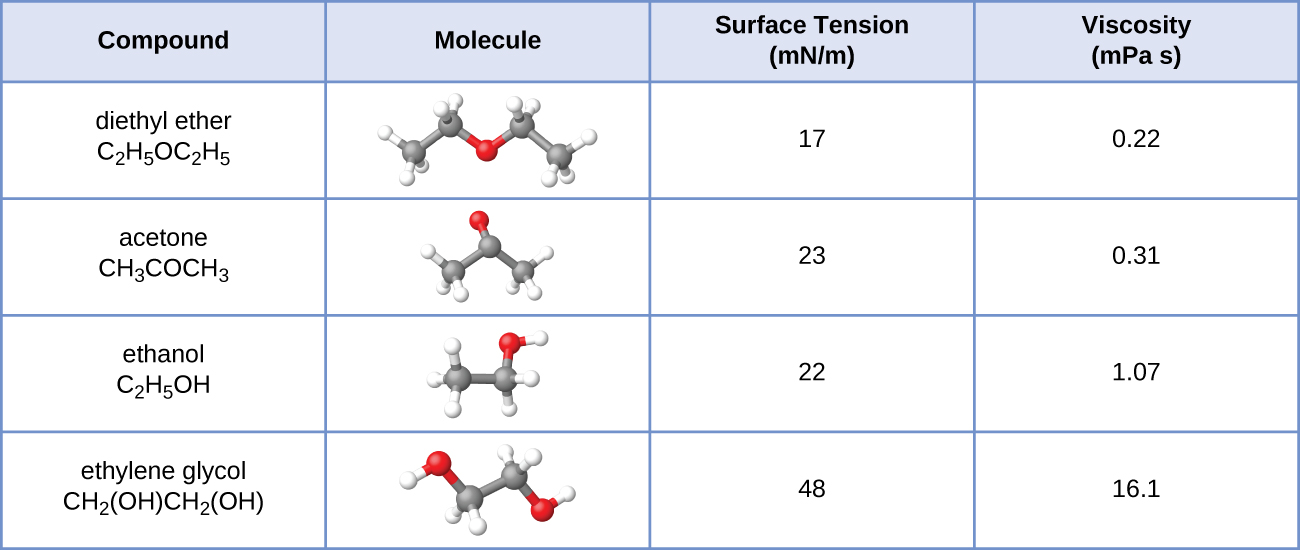
This table has four columns and five rows. The first row is a header row, and it labels each column:

(a) Explain their differences in viscosity in terms of the size and shape of their molecules and their IMFs.

(b) Explain their differences in surface tension in terms of the size and shape of their molecules and their IMFs:

Y'all may have heard someone use the figure of spoken language "slower than molasses in wintertime" to describe a process that occurs slowly. Explain why this is an apt idiom, using concepts of molecular size and shape, molecular interactions, and the effect of changing temperature.

Temperature has an issue on intermolecular forces: The higher the temperature, the greater the kinetic energies of the molecules and the greater the extent to which their intermolecular forces are overcome, and so the more fluid (less mucilaginous) the liquid. The lower the temperature, the less the intermolecular forces are overcome, and and then the less pasty the liquid.

It is frequently recommended that y'all let your automobile engine run idle to warm up before driving, particularly on cold wintertime days. While the benefit of prolonged idling is dubious, it is certainly true that a warm engine is more fuel efficient than a cold ane. Explicate the reason for this.

The surface tension and viscosity of h2o at several dissimilar temperatures are given in this table.

Water Surface Tension (mN/m) Viscosity (mPa south)
0 °C 75.6 1.79
twenty °C 72.eight i.00
60 °C 66.two 0.47
100 °C 58.9 0.28

(a) As temperature increases, what happens to the surface tension of water? Explain why this occurs, in terms of molecular interactions and the effect of irresolute temperature.

(b) Equally temperature increases, what happens to the viscosity of h2o? Explain why this occurs, in terms of molecular interactions and the effect of changing temperature.

(a) Equally the water reaches higher temperatures, the increased kinetic energies of its molecules are more than constructive in overcoming hydrogen bonding, and so its surface tension decreases. Surface tension and intermolecular forces are directly related. (b) The same tendency in viscosity is seen as in surface tension, and for the same reason.

At 25 °C, how high volition water rising in a drinking glass capillary tube with an inner bore of 0.63 mm? Refer to (Figure) for the required information.

H2o rises in a glass capillary tube to a height of 17 cm. What is the diameter of the capillary tube?

1.7 × 10−4 one thousand

Glossary

agglutinative force
forcefulness of attraction betwixt molecules of unlike chemic identities
capillary activity
flow of liquid within a porous material due to the attraction of the liquid molecules to the surface of the fabric and to other liquid molecules
cohesive strength
force of attraction between identical molecules
surface tension
energy required to increase the expanse, or length, of a liquid surface by a given amount
viscosity
measure out of a liquid's resistance to flow

warrenwered1973.blogspot.com

Source: https://opentextbc.ca/chemistry2eopenstax/chapter/properties-of-liquids/

0 Response to "Match the Following Properties of Liquids to What They Indicate About the Relative Strength"

Post a Comment

Subscribe to: Post Comments (Atom)

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel